Refine search
Actions for selected content:
22 results
Anti-Theists cannot have Theistic Faith
-
- Journal:
- Canadian Journal of Philosophy / Volume 54 / Issue 3 / April 2024
- Published online by Cambridge University Press:
- 24 April 2025, pp. 219-229
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
9 - Positivity of the CM Line Bundle
-
- Book:
- K-stability of Fano Varieties
- Published online:
- 08 May 2025
- Print publication:
- 24 April 2025, pp 323-364
-
- Chapter
- Export citation
Calling “Gevald”: on the emergence of negative election forecasts in partisan communications
-
- Journal:
- Experimental Economics / Volume 27 / Issue 4 / September 2024
- Published online by Cambridge University Press:
- 14 March 2025, pp. 787-819
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
37 - The Power of Positivity
- from Part IV - Caring For Your Soul
-
-
- Book:
- The Gift of Aging
- Published online:
- 08 June 2023
- Print publication:
- 08 June 2023, pp 253-256
-
- Chapter
- Export citation
36 - From Revolution to Pandemic
- from Part IV - Caring For Your Soul
-
-
- Book:
- The Gift of Aging
- Published online:
- 08 June 2023
- Print publication:
- 08 June 2023, pp 243-252
-
- Chapter
- Export citation
10 - 106 Proof
- from Part I - Caring For Your Mind
-
-
- Book:
- The Gift of Aging
- Published online:
- 08 June 2023
- Print publication:
- 08 June 2023, pp 64-68
-
- Chapter
- Export citation
Afterword
- from Part IV - Caring For Your Soul
-
-
- Book:
- The Gift of Aging
- Published online:
- 08 June 2023
- Print publication:
- 08 June 2023, pp 259-260
-
- Chapter
- Export citation
Norms on complex matrices induced by random vectors
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 66 / Issue 3 / September 2023
- Published online by Cambridge University Press:
- 23 December 2022, pp. 808-826
- Print publication:
- September 2023
-
- Article
- Export citation
29 - Finite Difference Methods for Hyperbolic Problems
- from Part V - Boundary and Initial Boundary Value Problems
-
- Book:
- Classical Numerical Analysis
- Published online:
- 29 September 2022
- Print publication:
- 20 October 2022, pp 811-836
-
- Chapter
- Export citation

The Increasing Viability of Good News
-
- Published online:
- 15 June 2021
- Print publication:
- 12 August 2021
-
- Element
- Export citation
Chapter 4 - Motivational Systems Theory
-
- Book:
- Motivating Self and Others
- Published online:
- 12 October 2020
- Print publication:
- 22 October 2020, pp 113-176
-
- Chapter
- Export citation
Analysis of a spatially inhomogeneous stochastic partial differential equation epidemic model
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 57 / Issue 2 / June 2020
- Published online by Cambridge University Press:
- 16 July 2020, pp. 613-636
- Print publication:
- June 2020
-
- Article
- Export citation
18 - Aging and Cognitive Functioning: The Impact of Goals and Motivation
- from Part III - Aging in a Socioemotional Context
-
-
- Book:
- The Cambridge Handbook of Cognitive Aging
- Published online:
- 28 May 2020
- Print publication:
- 28 May 2020, pp 332-349
-
- Chapter
- Export citation
Measures of irrationality for hypersurfaces of large degree
- Part of
-
- Journal:
- Compositio Mathematica / Volume 153 / Issue 11 / November 2017
- Published online by Cambridge University Press:
- 04 September 2017, pp. 2368-2393
- Print publication:
- November 2017
-
- Article
- Export citation
Theta bases are atomic
- Part of
-
- Journal:
- Compositio Mathematica / Volume 153 / Issue 6 / June 2017
- Published online by Cambridge University Press:
- 26 April 2017, pp. 1217-1219
- Print publication:
- June 2017
-
- Article
- Export citation
Divisorial Models of Normal Varieties
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 60 / Issue 4 / November 2017
- Published online by Cambridge University Press:
- 31 January 2017, pp. 1053-1064
-
- Article
- Export citation
ON A CLASS OF ELLIPTIC SYSTEM OF SCHRÖDINGER–POISSON TYPE
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 97 / Issue 3 / December 2014
- Published online by Cambridge University Press:
- 24 September 2014, pp. 301-314
- Print publication:
- December 2014
-
- Article
-
- You have access
- Export citation
Proof of a positivity conjecture of M. Kontsevich on non-commutative cluster variables
- Part of
-
- Journal:
- Compositio Mathematica / Volume 148 / Issue 6 / November 2012
- Published online by Cambridge University Press:
- 31 October 2012, pp. 1821-1832
- Print publication:
- November 2012
-
- Article
-
- You have access
- Export citation
ON THE POSITIVITY OF RIEMANN–STIELTJES INTEGRALS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 87 / Issue 3 / June 2013
- Published online by Cambridge University Press:
- 02 August 2012, pp. 400-405
- Print publication:
- June 2013
-
- Article
-
- You have access
- Export citation
Semigroup Analysis of Structured ParasitePopulations
-
- Journal:
- Mathematical Modelling of Natural Phenomena / Volume 5 / Issue 3 / 2010
- Published online by Cambridge University Press:
- 28 April 2010, pp. 94-114
- Print publication:
- 2010
-
- Article
- Export citation
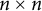
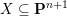

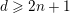
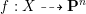
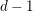
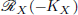 is finitely generated. We introduce a notion of nefness for non-ℚ-Gorenstein varieties and study some of its properties. We then focus on these properties for non-ℚ-Gorenstein toric varieties.
is finitely generated. We introduce a notion of nefness for non-ℚ-Gorenstein varieties and study some of its properties. We then focus on these properties for non-ℚ-Gorenstein toric varieties.