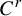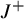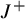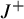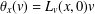Refine search
Actions for selected content:
7 results
CLASSIFICATION OF PERIODIC ORBITS FOR SQUARE AND RECTANGULAR BILLIARDS
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 67 / 2025
- Published online by Cambridge University Press:
- 08 October 2025, e33
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Distribution in homology classes and discrete fractal dimension
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 28 May 2024, pp. 1-8
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Similarities and differences between specification and non-uniform specification
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 12 / December 2024
- Published online by Cambridge University Press:
- 15 April 2024, pp. 3501-3529
- Print publication:
- December 2024
-
- Article
- Export citation
 $C^r$-chain closing lemma for certain partially hyperbolic diffeomorphisms
$C^r$-chain closing lemma for certain partially hyperbolic diffeomorphisms
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 7 / July 2024
- Published online by Cambridge University Press:
- 11 October 2023, pp. 1923-1944
- Print publication:
- July 2024
-
- Article
-
- You have access
- HTML
- Export citation
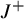 $J^+$-invariants for planar two-center Stark–Zeeman systems
$J^+$-invariants for planar two-center Stark–Zeeman systems
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 43 / Issue 7 / July 2023
- Published online by Cambridge University Press:
- 24 May 2022, pp. 2258-2292
- Print publication:
- July 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
CONTRACTIBLE PERIODIC ORBITS OF LAGRANGIAN SYSTEMS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 99 / Issue 3 / June 2019
- Published online by Cambridge University Press:
- 30 January 2019, pp. 445-453
- Print publication:
- June 2019
-
- Article
-
- You have access
- Export citation
Pairs of periodic orbits with fixed homology difference
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 53 / Issue 3 / October 2010
- Published online by Cambridge University Press:
- 12 August 2010, pp. 799-808
-
- Article
-
- You have access
- Export citation