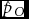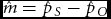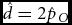Refine search
Actions for selected content:
2 results
A Note on Parameter Estimation for Lazarsfeld's Latent Class Analysis
-
- Journal:
- Psychometrika / Volume 43 / Issue 1 / March 1978
- Published online by Cambridge University Press:
- 01 January 2025, pp. 123-126
-
- Article
- Export citation
Statistical Analyses of Monozygotic and Dizygotic Twinning Rates
-
- Journal:
- Twin Research and Human Genetics / Volume 16 / Issue 6 / December 2013
- Published online by Cambridge University Press:
- 24 September 2013, pp. 1107-1111
-
- Article
-
- You have access
- HTML
- Export citation