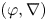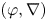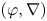Refine search
Actions for selected content:
8 results
Logarithmic growth filtrations for
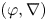 $(\varphi ,\nabla )$-modules over the bounded Robba ring
$(\varphi ,\nabla )$-modules over the bounded Robba ring
- Part of
-
- Journal:
- Compositio Mathematica / Volume 157 / Issue 6 / June 2021
- Published online by Cambridge University Press:
- 04 June 2021, pp. 1265-1301
- Print publication:
- June 2021
-
- Article
- Export citation
Corrigendum: Local and global structure of connections on nonarchimedean curves
- Part of
-
- Journal:
- Compositio Mathematica / Volume 153 / Issue 12 / December 2017
- Published online by Cambridge University Press:
- 13 September 2017, pp. 2658-2665
- Print publication:
- December 2017
-
- Article
-
- You have access
- HTML
- Export citation
Local and global structure of connections on nonarchimedean curves
- Part of
-
- Journal:
- Compositio Mathematica / Volume 151 / Issue 6 / June 2015
- Published online by Cambridge University Press:
- 07 January 2015, pp. 1096-1156
- Print publication:
- June 2015
-
- Article
- Export citation
Product formula for p -adic epsilon factors
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 14 / Issue 2 / April 2015
- Published online by Cambridge University Press:
- 08 May 2014, pp. 275-377
- Print publication:
- April 2015
-
- Article
- Export citation
On ramification filtrations and p-adic differential equations, II: mixed characteristic case
- Part of
-
- Journal:
- Compositio Mathematica / Volume 148 / Issue 2 / March 2012
- Published online by Cambridge University Press:
- 30 November 2011, pp. 415-463
- Print publication:
- March 2012
-
- Article
-
- You have access
- Export citation
Logarithmic growth and Frobenius filtrations for solutions of p-adic differential equations
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 8 / Issue 3 / July 2009
- Published online by Cambridge University Press:
- 18 February 2009, pp. 465-505
- Print publication:
- July 2009
-
- Article
- Export citation
p-adic confluence of q-difference equations
- Part of
-
- Journal:
- Compositio Mathematica / Volume 144 / Issue 4 / July 2008
- Published online by Cambridge University Press:
- 01 July 2008, pp. 867-919
- Print publication:
- July 2008
-
- Article
-
- You have access
- Export citation
Dwork’s conjecture on the logarithmic growth of solutions of p-adic differential equations
- Part of
-
- Journal:
- Compositio Mathematica / Volume 144 / Issue 2 / March 2008
- Published online by Cambridge University Press:
- 01 March 2008, pp. 484-494
- Print publication:
- March 2008
-
- Article
-
- You have access
- Export citation