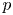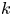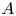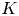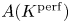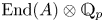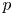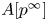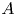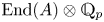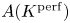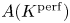Refine search
Actions for selected content:
3 results
Perfect points of abelian varieties
- Part of
-
- Journal:
- Compositio Mathematica / Volume 159 / Issue 11 / November 2023
- Published online by Cambridge University Press:
- 08 September 2023, pp. 2261-2278
- Print publication:
- November 2023
-
- Article
- Export citation
BETTI NUMBER ESTIMATES IN
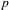 $p$-ADIC COHOMOLOGY
$p$-ADIC COHOMOLOGY
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 18 / Issue 5 / September 2019
- Published online by Cambridge University Press:
- 07 August 2017, pp. 957-991
- Print publication:
- September 2019
-
- Article
- Export citation
Stabilité de l’holonomie sur les variétés quasi-projectives
- Part of
-
- Journal:
- Compositio Mathematica / Volume 147 / Issue 6 / November 2011
- Published online by Cambridge University Press:
- 24 August 2011, pp. 1772-1792
- Print publication:
- November 2011
-
- Article
-
- You have access
- Export citation