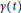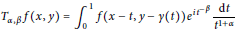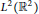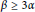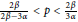Refine search
Actions for selected content:
1 results
The Oscillatory Hyper-Hilbert Transform Associated with Plane Curves
-
- Journal:
- Canadian Mathematical Bulletin / Volume 61 / Issue 4 / 01 December 2018
- Published online by Cambridge University Press:
- 20 November 2018, pp. 802-811
- Print publication:
- 01 December 2018
-
- Article
-
- You have access
- Export citation
-
In this paper, the bounded properties of oscillatory hyper-Hilbert transformalong certain plane curves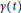
$\gamma \left( t \right)$ ,
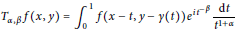$${{T}_{\alpha ,\beta }}f\left( x,\,y \right)\,=\,\int_{0}^{1}{f\left( x\,-\,t,\,y\,-\,\gamma \left( t \right) \right){{e}^{i{{t}^{-\beta }}}}\frac{\text{d}t}{{{t}^{1}}+\alpha }}$$are studied. For general curves, these operators are bounded in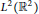
${{L}^{2}}\left( {{\mathbb{R}}^{2}} \right)$ if 
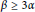$\beta \,\ge \,3\alpha $ . Their boundedness in 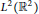${{L}^{p}}\left( {{\mathbb{R}}^{2}} \right)$ is also obtained, whenever 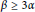$\beta \,\ge \,3\alpha $ and 
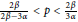$\frac{2\beta }{2\beta -3\alpha }\,<\,p\,<\,\frac{2\beta }{3\alpha }$ .
