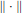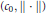Skip to main content Accessibility help
×
  1. Home
  2. Search

Refine search

Refine search

Access:
Content type:
Publication date:
Apply   From and To filters
Subject: Show more
Journals Show more
Publishers: Show more
Societies Show more
Series: Show more
Collections: Show more

Actions for selected content:

Select all | Deselect all
  • View selected items
  • Export citations
  • Download PDF (zip)
  • Save to Kindle
  • Save to Dropbox
  • Save to Google Drive

Save Search

You can save your searches here and later view and run them again in "My saved searches".

Please provide a title, maximum of 40 characters.
Cancel
×

2 results

  • 4 - Subspaces, Rank, and Nearest-Subspace Classification

  • Jeffrey A. Fessler, University of Michigan, Ann Arbor, Raj Rao Nadakuditi, University of Michigan, Ann Arbor
  • Book:
    Linear Algebra for Data Science, Machine Learning, and Signal Processing
    Published online:
    01 November 2024
    Print publication:
    16 May 2024, pp 96-142

  • Summary

    An important operation in signal processing and machine learning is dimensionality reduction. There are many such methods, but the starting point is usually linear methods that map data to a lower-dimensional set called a subspace. When working with matrices, the notion of dimension is quantified by rank. This chapter reviews subspaces, span, dimension, rank, and nullspace. These linear algebra concepts are crucial to thoroughly understanding the SVD, a primary tool for the rest of the book (and beyond). The chapter concludes with a machine learning application, signal classification by nearest subspace, that builds on all the concepts of the chapter.

  • New Examples of Non-Archimedean Banach Spaces and Applications

  • C. Perez-Garcia, W. H. Schikhof
  • Journal:
    Canadian Mathematical Bulletin / Volume 55 / Issue 4 / 01 December 2012
    Published online by Cambridge University Press:
    20 November 2018, pp. 821-829
    Print publication:
    01 December 2012
    • Article
      • You have access
    • PDF
    • Export citation

  • The study carried out in this paper about some new examples of Banach spaces, consisting of certain valued fields extensions, is a typical non-archimedean feature. We determine whether these extensions are of countable type, have $t$ -orthogonal bases, or are reflexive. As an application we construct, for a class of base fields, a norm 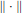$\left\| \,.\, \right\|$ on ${{c}_{0}}$ , equivalent to the canonical supremum norm, without non-zero vectors that are 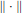$\left\| \,.\, \right\|$ -orthogonal and such that there is a multiplication on ${{c}_{0}}$ making 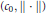$\left( {{c}_{0}},\,\left\| \,.\, \right\| \right)$ into a valued field.