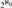Refine search
Actions for selected content:
11 results
5 - The Two-Body Problem
-
- Book:
- Classical Mechanics
- Published online:
- 26 June 2025
- Print publication:
- 19 June 2025, pp 95-135
-
- Chapter
- Export citation
2 - Mega-constellations
-
- Book:
- Who Owns Outer Space?
- Published online:
- 06 April 2023
- Print publication:
- 13 April 2023, pp 46-76
-
- Chapter
-
- You have access
- Open access
- HTML
- Export citation
7 - Gravitation
- from Part II
-
- Book:
- Modern Classical Mechanics
- Published online:
- 30 November 2020
- Print publication:
- 10 December 2020, pp 275-313
-
- Chapter
- Export citation
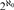 ${2^{{\aleph _0}}}$ PAIRWISE NONISOMORPHIC MAXIMAL-CLOSED SUBGROUPS OF SYM(ℕ) VIA THE CLASSIFICATION OF THE REDUCTS OF THE HENSON DIGRAPHS
${2^{{\aleph _0}}}$ PAIRWISE NONISOMORPHIC MAXIMAL-CLOSED SUBGROUPS OF SYM(ℕ) VIA THE CLASSIFICATION OF THE REDUCTS OF THE HENSON DIGRAPHS
-
- Journal:
- The Journal of Symbolic Logic / Volume 83 / Issue 2 / June 2018
- Published online by Cambridge University Press:
- 01 August 2018, pp. 395-415
- Print publication:
- June 2018
-
- Article
- Export citation
Meteor Databases in Astronomy
-
- Journal:
- Proceedings of the International Astronomical Union / Volume 12 / Issue S325 / October 2016
- Published online by Cambridge University Press:
- 30 May 2017, pp. 389-392
- Print publication:
- October 2016
-
- Article
-
- You have access
- Export citation
Some Remarks Concerning the Topological Characterization of Limit Sets for Surface Flows
-
- Journal:
- Canadian Mathematical Bulletin / Volume 54 / Issue 2 / 01 June 2011
- Published online by Cambridge University Press:
- 20 November 2018, pp. 311-315
- Print publication:
- 01 June 2011
-
- Article
-
- You have access
- Export citation
EXPANSION OF ORBITS OF SOME DYNAMICAL SYSTEMS OVER FINITE FIELDS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 82 / Issue 2 / October 2010
- Published online by Cambridge University Press:
- 07 April 2010, pp. 232-239
- Print publication:
- October 2010
-
- Article
-
- You have access
- Export citation
Generalizations of Frobenius’ Theorem on Manifolds and Subcartesian Spaces
-
- Journal:
- Canadian Mathematical Bulletin / Volume 50 / Issue 3 / 01 September 2007
- Published online by Cambridge University Press:
- 20 November 2018, pp. 447-459
- Print publication:
- 01 September 2007
-
- Article
-
- You have access
- Export citation
On-the-Fly Prediction of Orbit Corrections for RTK Positioning
-
- Journal:
- The Journal of Navigation / Volume 59 / Issue 2 / May 2006
- Published online by Cambridge University Press:
- 06 April 2006, pp. 321-334
- Print publication:
- May 2006
-
- Article
- Export citation
Investigating a self-consistent galactic potential with central mass
-
- Journal:
- Symposium - International Astronomical Union / Volume 153 / 1993
- Published online by Cambridge University Press:
- 07 August 2017, pp. 385-386
- Print publication:
- 1993
-
- Article
-
- You have access
- Export citation