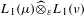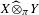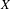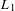Refine search
Actions for selected content:
2 results
DAUGAVET PROPERTY IN TENSOR PRODUCT SPACES
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 20 / Issue 4 / July 2021
- Published online by Cambridge University Press:
- 21 November 2019, pp. 1409-1428
- Print publication:
- July 2021
-
- Article
- Export citation
Octahedrality in Lipschitz-free Banach spaces
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 148 / Issue 3 / June 2018
- Published online by Cambridge University Press:
- 28 December 2017, pp. 447-460
- Print publication:
- June 2018
-
- Article
- Export citation