Refine search
Actions for selected content:
2 results
REVERSE MATHEMATICS OF FIRST-ORDER THEORIES WITH FINITELY MANY MODELS
-
- Journal:
- The Journal of Symbolic Logic / Volume 79 / Issue 3 / September 2014
- Published online by Cambridge University Press:
- 18 August 2014, pp. 955-984
- Print publication:
- September 2014
-
- Article
- Export citation
On inverse γ-systems and the number of L∞λ-equivalent, non-isomorphic models for λ singular
-
- Journal:
- The Journal of Symbolic Logic / Volume 65 / Issue 1 / March 2000
- Published online by Cambridge University Press:
- 12 March 2014, pp. 272-284
- Print publication:
- March 2000
-
- Article
- Export citation
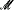 of cardinality λ, let No(
of cardinality λ, let No(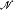 of cardinality λ which are
of cardinality λ which are  of abelian groups and their certain kind of quotient limits Gr(
of abelian groups and their certain kind of quotient limits Gr(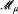 , of cardinality λ with No(
, of cardinality λ with No(