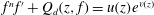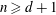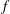Refine search
Actions for selected content:
6 results
ON SOLUTIONS TO NONHOMOGENEOUS ALGEBRAIC DIFFERENTIAL EQUATIONS AND THEIR APPLICATION
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 97 / Issue 3 / December 2014
- Published online by Cambridge University Press:
- 24 September 2014, pp. 391-403
- Print publication:
- December 2014
-
- Article
-
- You have access
- Export citation
A non-Archimedean Montel’s theorem
- Part of
-
- Journal:
- Compositio Mathematica / Volume 148 / Issue 3 / May 2012
- Published online by Cambridge University Press:
- 21 February 2012, pp. 966-990
- Print publication:
- May 2012
-
- Article
-
- You have access
- Export citation
On the value distribution of f2f(k)
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 78 / Issue 1 / February 2005
- Published online by Cambridge University Press:
- 09 April 2009, pp. 17-26
- Print publication:
- February 2005
-
- Article
-
- You have access
- Export citation
Normality and exceptional functions of derivatives
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 76 / Issue 3 / June 2004
- Published online by Cambridge University Press:
- 09 April 2009, pp. 403-414
- Print publication:
- June 2004
-
- Article
-
- You have access
- Export citation
Some Convergence Results for p-Harmonic Functions on Metric Measure Spaces
-
- Journal:
- Proceedings of the London Mathematical Society / Volume 87 / Issue 1 / July 2003
- Published online by Cambridge University Press:
- 25 June 2003, pp. 226-246
- Print publication:
- July 2003
-
- Article
- Export citation
On normal families of meromorphic functions
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 74 / Issue 2 / April 2003
- Published online by Cambridge University Press:
- 09 April 2009, pp. 155-164
- Print publication:
- April 2003
-
- Article
-
- You have access
- Export citation