Refine search
Actions for selected content:
2 results
Ancient multiple-layer solutions to the Allen–Cahn equation
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 148 / Issue 6 / December 2018
- Published online by Cambridge University Press:
- 18 December 2017, pp. 1165-1199
- Print publication:
- December 2018
-
- Article
- Export citation
Numerical Analysis for a Nonlocal Parabolic Problem
- Part of
-
- Journal:
- East Asian Journal on Applied Mathematics / Volume 6 / Issue 4 / November 2016
- Published online by Cambridge University Press:
- 19 October 2016, pp. 434-447
- Print publication:
- November 2016
-
- Article
- Export citation
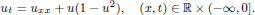
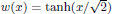 connects, as a ‘transition layer’, the stable phases –1 and +1. We construct a solution
connects, as a ‘transition layer’, the stable phases –1 and +1. We construct a solution