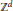We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We study the asymptotic behaviour of random walks in i.i.d. random environments on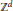 
${{\mathbb{Z}}^{d}}$. The environments need not be elliptic, so some steps may not be available to the random walker. We prove a monotonicity result for the velocity (when it exists) for any 2-valued environment, and show that this does not hold for 3-valued environments without additional assumptions. We give a proof of directional transience and the existence of positive speeds under strong but non-trivial conditions on the distribution of the environment. Our results include generalisations (to the non-elliptic setting) of 0-1 laws for directional transience and, in 2-dimensions, the existence of a deterministic limiting velocity.
