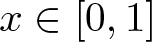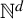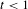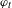Refine search
Actions for selected content:
9 results
Multivariate multifractal analysis of Lévy functions. Part I: Determination of multifractal spectra
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 13 January 2026, pp. 1-32
-
- Article
- Export citation
3 - Gaussian Multiplicative Chaos
-
- Book:
- Gaussian Free Field and Liouville Quantum Gravity
- Published online:
- 20 November 2025
- Print publication:
- 04 December 2025, pp 75-132
-
- Chapter
- Export citation
Birkhoff spectrum for diagonally self-affine sets and digit frequencies for GLS systems with redundancy
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 09 December 2024, pp. 1-26
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Multifractal analysis of homological growth rates for hyperbolic surfaces
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 3 / March 2025
- Published online by Cambridge University Press:
- 18 September 2024, pp. 849-883
- Print publication:
- March 2025
-
- Article
- Export citation
Hausdorff dimension of multidimensional multiplicative subshifts
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 5 / May 2024
- Published online by Cambridge University Press:
- 19 July 2023, pp. 1239-1268
- Print publication:
- May 2024
-
- Article
- Export citation
Legal systems and stock market efficiency: an empirical analysis of stock indices around the world
-
- Journal:
- Journal of Institutional Economics / Volume 19 / Issue 4 / August 2023
- Published online by Cambridge University Press:
- 17 March 2023, pp. 459-477
-
- Article
- Export citation
Geometric and combinatorial properties of self-similar multifractal measures
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 43 / Issue 6 / June 2023
- Published online by Cambridge University Press:
- 27 April 2022, pp. 2028-2072
- Print publication:
- June 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Unique equilibrium states, large deviations and Lyapunov spectra for the Katok map
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 7 / July 2021
- Published online by Cambridge University Press:
- 20 March 2020, pp. 2182-2219
- Print publication:
- July 2021
-
- Article
- Export citation
Multidimensional Models for Methodological Validation in MultifractalAnalysis
-
- Journal:
- Mathematical Modelling of Natural Phenomena / Volume 3 / Issue 6 / 2008
- Published online by Cambridge University Press:
- 24 December 2008, pp. 33-47
- Print publication:
- 2008
-
- Article
- Export citation