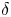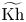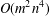Refine search
Actions for selected content:
2 results
Thin links and Conway spheres
- Part of
-
- Journal:
- Compositio Mathematica / Volume 160 / Issue 7 / July 2024
- Published online by Cambridge University Press:
- 20 May 2024, pp. 1467-1524
- Print publication:
- July 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
INTERSECTIONS OF MULTICURVES FROM DYNNIKOV COORDINATES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 98 / Issue 1 / August 2018
- Published online by Cambridge University Press:
- 03 May 2018, pp. 149-158
- Print publication:
- August 2018
-
- Article
-
- You have access
- Export citation