We show that the sequence of moments of order less than 1 of averages of i.i.d. positive random variables is log-concave. For moments of order at least 1, we conjecture that the sequence is log-convex and show that this holds eventually for integer moments (after neglecting the first 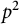 $p^2$
terms of the sequence).
$p^2$
terms of the sequence).