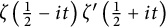Refine search
Actions for selected content:
3 results
Lambert series of logarithm, the derivative of Deninger’s function
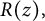 $R(z),$ and a mean value theorem for
$R(z),$ and a mean value theorem for 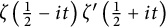 $\zeta \left (\frac {1}{2}-it\right )\zeta '\left (\frac {1}{2}+it\right )$
$\zeta \left (\frac {1}{2}-it\right )\zeta '\left (\frac {1}{2}+it\right )$
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 76 / Issue 5 / October 2024
- Published online by Cambridge University Press:
- 11 October 2023, pp. 1695-1730
- Print publication:
- October 2024
-
- Article
- Export citation
AN ALTERNATIVE APPROACH TO FRÉCHET DERIVATIVES
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 111 / Issue 2 / October 2021
- Published online by Cambridge University Press:
- 14 May 2020, pp. 202-220
- Print publication:
- October 2021
-
- Article
- Export citation
Simple zeros of the Riemann zeta-function
-
- Journal:
- Proceedings of the London Mathematical Society / Volume 76 / Issue 3 / May 1998
- Published online by Cambridge University Press:
- 01 May 1998, pp. 497-522
- Print publication:
- May 1998
-
- Article
- Export citation