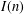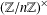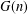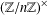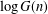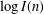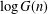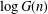Refine search
Actions for selected content:
2 results
On elements of prescribed norm in maximal orders of a quaternion algebra
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 11 November 2024, pp. 1-28
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
-
Let
$\mathcal {O}$ be a maximal order in the quaternion algebra over 
$\mathbb Q$ ramified at p and 
$\infty $. We prove two theorems that allow us to recover the structure of 
$\mathcal {O}$ from limited information. The first says that for any infinite set S of integers coprime to p, 
$\mathcal {O}$ is spanned as a 
${\mathbb {Z}}$-module by elements with norm in S. The second says that 
$\mathcal {O}$ is determined up to isomorphism by its theta function.
THE DISTRIBUTION OF THE NUMBER OF SUBGROUPS OF THE MULTIPLICATIVE GROUP
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 108 / Issue 1 / February 2020
- Published online by Cambridge University Press:
- 21 December 2018, pp. 46-97
- Print publication:
- February 2020
-
- Article
-
- You have access
- Export citation
-
Let
$I(n)$ denote the number of isomorphism classes of subgroups of 
$(\mathbb{Z}/n\mathbb{Z})^{\times }$, and let 
$G(n)$ denote the number of subgroups of 
$(\mathbb{Z}/n\mathbb{Z})^{\times }$ counted as sets (not up to isomorphism). We prove that both 
$\log G(n)$ and 
$\log I(n)$ satisfy Erdős–Kac laws, in that suitable normalizations of them are normally distributed in the limit. Of note is that 
$\log G(n)$ is not an additive function but is closely related to the sum of squares of additive functions. We also establish the orders of magnitude of the maximal orders of 
$\log G(n)$ and 
$\log I(n)$.
