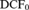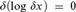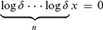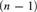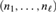Refine search
Actions for selected content:
3 results
Appendix F - Complex Function Theory
-
- Book:
- Bounded Gaps Between Primes
- Published online:
- 10 September 2021
- Print publication:
- 25 February 2021, pp 516-521
-
- Chapter
- Export citation
CONSTRUCTING TYPES IN DIFFERENTIALLY CLOSED FIELDS THAT ARE ANALYSABLE IN THE CONSTANTS
-
- Journal:
- The Journal of Symbolic Logic / Volume 83 / Issue 4 / December 2018
- Published online by Cambridge University Press:
- 21 December 2018, pp. 1413-1433
- Print publication:
- December 2018
-
- Article
- Export citation
SHARP LOGARITHMIC DERIVATIVE ESTIMATES WITH APPLICATIONS TO ORDINARY DIFFERENTIAL EQUATIONS IN THE UNIT DISC
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 88 / Issue 2 / April 2010
- Published online by Cambridge University Press:
- 07 April 2010, pp. 145-167
- Print publication:
- April 2010
-
- Article
-
- You have access
- Export citation