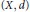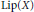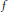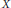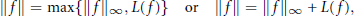Let 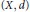$(X,\,d)$ be a metric space, and let 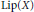$\text{Lip(}X\text{)}$ denote the Banach space of all scalar-valued bounded Lipschitz functions 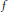$f$ on 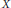$X$ endowed with one of the natural norms

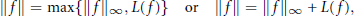$$\left\| f \right\|\,=\,\max \{{{\left\| f \right\|}_{\infty }},\,L(f)\}\,\,\text{or}\,\,\left\| f \right\|\,=\,{{\left\| f \right\|}_{\infty }}\,+\,L(f),$$

where 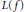$L(f)$ is the Lipschitz constant of 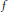$f$ . It is said that the isometry group of 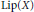$\text{Lip(}X\text{)}$ is canonical if every surjective linear isometry of 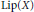$\text{Lip(}X\text{)}$ is induced by a surjective isometry of 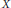$X$ . In this paper we prove that if 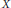$X$ is bounded separable and the isometry group of 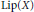$\text{Lip(}X\text{)}$ is canonical, then every 2-local isometry of 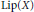$\text{Lip(}X\text{)}$ is a surjective linear isometry. Furthermore, we give a complete description of all 2-local isometries of 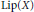$\text{Lip(}X\text{)}$ when 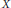$X$ is bounded.

As a consequence of the main result of the paper we obtain that every 2-local isometry of the $C^*$-algebra $B(H)$ of all bounded linear operators on a separable infinite-dimensional Hilbert space $H$ is an isometry. We have a similar statement concerning the isometries of any extension of the algebra of all compact operators by a separable commutative $C^*$-algebra. Therefore, on those $C^*$-algebras the isometries are completely determined by their local actions on the two-point subsets of the underlying algebras.

AMS 2000 Mathematics subject classification: Primary 47B49