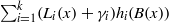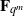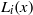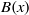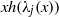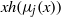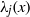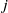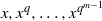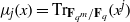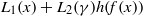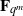We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
In this paper, we construct several new permutation polynomials over finite fields. First, using the linearised polynomials, we construct the permutation polynomial of the form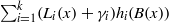 
${ \mathop{\sum }\nolimits}_{i= 1}^{k} ({L}_{i} (x)+ {\gamma }_{i} ){h}_{i} (B(x))$ over 
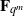${\mathbf{F} }_{{q}^{m} } $, where 
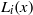${L}_{i} (x)$ and 
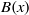$B(x)$ are linearised polynomials. This extends a theorem of Coulter, Henderson and Matthews. Consequently, we generalise a result of Marcos by constructing permutation polynomials of the forms 
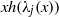$xh({\lambda }_{j} (x))$ and 
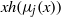$xh({\mu }_{j} (x))$, where 
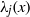${\lambda }_{j} (x)$ is the 
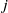$j$th elementary symmetric polynomial of 
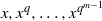$x, {x}^{q} , \ldots , {x}^{{q}^{m- 1} } $ and 
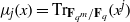${\mu }_{j} (x)= {\mathrm{Tr} }_{{\mathbf{F} }_{{q}^{m} } / {\mathbf{F} }_{q} } ({x}^{j} )$. This answers an open problem raised by Zieve in 2010. Finally, by using the linear translator, we construct the permutation polynomial of the form 
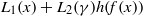${L}_{1} (x)+ {L}_{2} (\gamma )h(f(x))$ over 
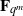${\mathbf{F} }_{{q}^{m} } $, which extends a result of Kyureghyan.
