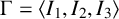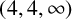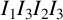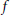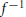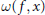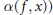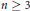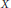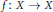Refine search
Actions for selected content:
4 results
On quasiconformal non-equivalence of gasket Julia sets and limit sets
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 11 / November 2025
- Published online by Cambridge University Press:
- 09 June 2025, pp. 3465-3489
- Print publication:
- November 2025
-
- Article
- Export citation
ON THE LIMIT SET OF A COMPLEX HYPERBOLIC TRIANGLE GROUP
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 110 / Issue 2 / October 2024
- Published online by Cambridge University Press:
- 02 February 2024, pp. 338-345
- Print publication:
- October 2024
-
- Article
- Export citation
Addendum to “Limit Sets of Typical Homeomorphisms”
-
- Journal:
- Canadian Mathematical Bulletin / Volume 57 / Issue 2 / 14 June 2014
- Published online by Cambridge University Press:
- 20 November 2018, pp. 240-244
- Print publication:
- 14 June 2014
-
- Article
-
- You have access
- Export citation
Limit Sets of Typical Homeomorphisms
-
- Journal:
- Canadian Mathematical Bulletin / Volume 55 / Issue 2 / 01 June 2012
- Published online by Cambridge University Press:
- 20 November 2018, pp. 225-232
- Print publication:
- 01 June 2012
-
- Article
-
- You have access
- Export citation