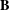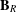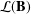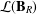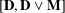Refine search
Actions for selected content:
2 results
Minimal monoids generating varieties with complex subvariety lattices
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 67 / Issue 2 / May 2024
- Published online by Cambridge University Press:
- 22 March 2024, pp. 617-642
-
- Article
- Export citation
THE LATTICE OF VARIETIES OF STRICT LEFT RESTRICTION SEMIGROUPS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 106 / Issue 1 / February 2019
- Published online by Cambridge University Press:
- 30 May 2018, pp. 31-55
- Print publication:
- February 2019
-
- Article
-
- You have access
- Export citation