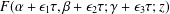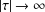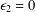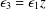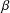Refine search
Actions for selected content:
2 results
14 - Algebraic Families, Dimension Counting, and Ruled Surfaces
-
- Book:
- Polynomial Methods and Incidence Theory
- Published online:
- 17 March 2022
- Print publication:
- 24 March 2022, pp 204-224
-
- Chapter
- Export citation
ASYMPTOTICS OF A GAUSS HYPERGEOMETRIC FUNCTION WITH TWO LARGE PARAMETERS: A NEW CASE
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 62 / Issue 4 / October 2020
- Published online by Cambridge University Press:
- 10 December 2019, pp. 446-452
-
- Article
-
- You have access
- Export citation