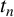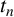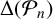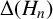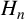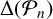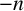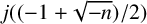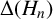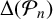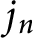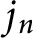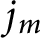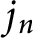Refine search
Actions for selected content:
4 results
ON DISCRIMINANTS OF MINIMAL POLYNOMIALS OF THE RAMANUJAN
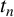 $t_n$ CLASS INVARIANTS
$t_n$ CLASS INVARIANTS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 108 / Issue 2 / October 2023
- Published online by Cambridge University Press:
- 11 April 2023, pp. 264-275
- Print publication:
- October 2023
-
- Article
- Export citation
Stieltjes interlacing of the zeros of
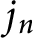 $j_n$
$j_n$
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 65 / Issue 4 / December 2022
- Published online by Cambridge University Press:
- 13 January 2022, pp. 976-993
- Print publication:
- December 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Special curves in modular surfaces
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 66 / Issue 1 / March 2023
- Published online by Cambridge University Press:
- 02 December 2021, pp. 1-18
- Print publication:
- March 2023
-
- Article
- Export citation
Generically split projective homogeneous varieties. II
-
- Journal:
- Journal of K-Theory / Volume 10 / Issue 1 / August 2012
- Published online by Cambridge University Press:
- 07 February 2012, pp. 1-8
- Print publication:
- August 2012
-
- Article
- Export citation