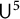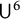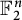Refine search
Actions for selected content:
2 results
Quantitative inverse theorem for Gowers uniformity norms
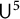 $\mathsf {U}^5$ and
$\mathsf {U}^5$ and 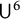 $\mathsf {U}^6$ in
$\mathsf {U}^6$ in 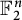 $\mathbb {F}_2^n$
$\mathbb {F}_2^n$
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 76 / Issue 4 / August 2024
- Published online by Cambridge University Press:
- 15 June 2023, pp. 1289-1338
- Print publication:
- August 2024
-
- Article
- Export citation
Direct and inverse results for popular differences in trees of positive dimension
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 2 / February 2024
- Published online by Cambridge University Press:
- 05 April 2023, pp. 481-508
- Print publication:
- February 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation