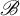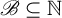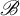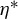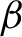Refine search
Actions for selected content:
3 results
Invariant measures for
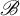 $\mathscr {B}$-free systems revisited
$\mathscr {B}$-free systems revisited
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 10 / October 2024
- Published online by Cambridge University Press:
- 08 March 2024, pp. 2901-2932
- Print publication:
- October 2024
-
- Article
- Export citation
Measures of maximal entropy of bounded density shifts
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 10 / October 2024
- Published online by Cambridge University Press:
- 20 February 2024, pp. 2960-2974
- Print publication:
- October 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On subshifts with slow forbidden word growth
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 42 / Issue 4 / April 2022
- Published online by Cambridge University Press:
- 12 January 2021, pp. 1487-1516
- Print publication:
- April 2022
-
- Article
-
- You have access
- Open access
- Export citation