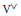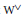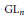Refine search
Actions for selected content:
5 results
The sequential loss of allelic diversity
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 50 / Issue A / December 2018
- Published online by Cambridge University Press:
- 01 February 2019, pp. 13-29
- Print publication:
- December 2018
-
- Article
-
- You have access
- Export citation
Types et contragrédientes
-
- Journal:
- Canadian Journal of Mathematics / Volume 66 / Issue 6 / 01 December 2014
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1287-1304
- Print publication:
- 01 December 2014
-
- Article
-
- You have access
- Export citation
Duality and intertwining for discrete Markov kernels: relations and examples
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 43 / Issue 2 / June 2011
- Published online by Cambridge University Press:
- 01 July 2016, pp. 437-460
- Print publication:
- June 2011
-
- Article
-
- You have access
- Export citation
On absorption times and Dirichlet eigenvalues
-
- Journal:
- ESAIM: Probability and Statistics / Volume 14 / 2010
- Published online by Cambridge University Press:
- 10 May 2010, pp. 117-150
- Print publication:
- 2010
-
- Article
- Export citation
Hecke algebras and ${\rm SL}_n$-types
-
- Journal:
- Proceedings of the London Mathematical Society / Volume 90 / Issue 1 / January 2005
- Published online by Cambridge University Press:
- 16 December 2004, pp. 87-131
- Print publication:
- January 2005
-
- Article
- Export citation