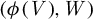Refine search
Actions for selected content:
5 results
A linear AFL for quaternion algebras
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 04 March 2025, pp. 1-23
-
- Article
- Export citation
On the linear AFL: the non-basic case
- Part of
-
- Journal:
- Compositio Mathematica / Volume 161 / Issue 2 / February 2025
- Published online by Cambridge University Press:
- 23 June 2025, pp. 385-425
- Print publication:
- February 2025
-
- Article
- Export citation
1 - The Minimal Model Program
-
- Book:
- Complex Algebraic Threefolds
- Published online:
- 29 September 2023
- Print publication:
- 19 October 2023, pp 1-58
-
- Chapter
- Export citation
BOUNDNESS OF INTERSECTION NUMBERS FOR ACTIONS BY TWO-DIMENSIONAL BIHOLOMORPHISMS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 21 / Issue 5 / September 2022
- Published online by Cambridge University Press:
- 22 January 2021, pp. 1677-1700
- Print publication:
- September 2022
-
- Article
- Export citation
Note on the Grothendieck Group of Subspaces of Rational Functions and Shokurov's Cartier b-divisors
-
- Journal:
- Canadian Mathematical Bulletin / Volume 57 / Issue 3 / 01 September 2014
- Published online by Cambridge University Press:
- 20 November 2018, pp. 562-572
- Print publication:
- 01 September 2014
-
- Article
-
- You have access
- Export citation