Refine search
Actions for selected content:
3 results
Soviet Inflection Points—A Play in Three Acts
-
- Journal:
- International Labor and Working-Class History / Volume 106 / October 2024
- Published online by Cambridge University Press:
- 11 October 2024, pp. 378-390
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Thin-layer solutions of the Helmholtz equation
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 32 / Issue 5 / October 2021
- Published online by Cambridge University Press:
- 06 October 2020, pp. 769-783
-
- Article
- Export citation
Inflection Points of Bessel Functions of Negative Order
-
- Journal:
- Canadian Journal of Mathematics / Volume 43 / Issue 6 / 01 December 1991
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1309-1322
- Print publication:
- 01 December 1991
-
- Article
-
- You have access
- Export citation
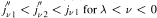 and
and 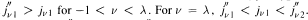 . Moreover,
. Moreover, 