We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
Drawing on an analogy with temporal fixpoint logic, we relate the
arithmetic fixpoint definable sets to the winning positions of certain
games, namely games whose winning conditions lie in the difference
hierarchy over $\Sigma^0_2$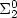
. This both provides a simple characterization
of the fixpoint hierarchy, and refines existing results on the power of
the game quantifier in descriptive set theory. We raise the problem of
transfinite fixpoint hierarchies.
