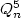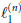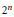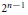Refine search
Actions for selected content:
2 results
Cycle and Path Embedding on 5-ary N-cubes
-
- Journal:
- RAIRO - Theoretical Informatics and Applications / Volume 43 / Issue 1 / January 2009
- Published online by Cambridge University Press:
- 28 February 2008, pp. 133-144
- Print publication:
- January 2009
-
- Article
- Export citation
On Locating Isometric 𝓁 (n) 1
-
- Journal:
- Canadian Mathematical Bulletin / Volume 44 / Issue 3 / 01 September 2001
- Published online by Cambridge University Press:
- 20 November 2018, pp. 370-375
- Print publication:
- 01 September 2001
-
- Article
-
- You have access
- Export citation