No CrossRef data available.
Article contents
On Locating Isometric 𝓁 (n) 1
Published online by Cambridge University Press: 20 November 2018
Abstract
Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.
Motivated by a question of Per Enflo, we develop a hypercube criterion for locating linear isometric copies of 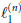 $\ell _{1}^{\left( n \right)}$ in an arbitrary real normed space
$\ell _{1}^{\left( n \right)}$ in an arbitrary real normed space 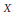 $X$ .
$X$ .
The said criterion involves finding 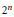 ${{2}^{n}}$ points in
${{2}^{n}}$ points in 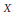 $X$ that satisfy one metric equality. This contrasts nicely to the standard classical criterion wherein one seeks
$X$ that satisfy one metric equality. This contrasts nicely to the standard classical criterion wherein one seeks  $n$ points that satisfy
$n$ points that satisfy 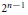 ${{2}^{n-1}}$ metric equalities.
${{2}^{n-1}}$ metric equalities.
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 2001
References
[BMW]
Bourgain, J., Milman, V. and Wolfson, H., On type of metric spaces. Trans. Amer.Math. Soc. 294 (1986), 295–317.Google Scholar
[DL]
Deza, M. M. and Laurent, M., Geometry of Cuts and Metrics. Algorithms and Combinatorics 15(1997), Springer Verlag, 1–600.Google Scholar
[E]
Enflo, P., On the non-existence of uniform homeomorphisms between Lp-spaces. Ark.Mat. 8 (1969), 103–105.Google Scholar
[LTW1]
Lennard, C., Tonge, A. and Weston, A., Generalized roundness and negative type. Michigan J. Math. 44 (1997), 37–45.Google Scholar
[LTW2]
Lennard, C., Tonge, A. and Weston, A., Roundness and metric type. J. Math. Anal. Appl. (to appear in 2000), 1–10.Google Scholar
[L]
Lövblom, G.-M., Uniform homeomorphisms between unit balls in Lp-spaces, Math. Scand. 62 (1988), 294–302.Google Scholar
[P]
Pisier, G., Probabilistic Methods in the Geometry of Banach Spaces. Springer LectureNotes in Math. 1206 (1985), 1–75.Google Scholar

