Refine search
Actions for selected content:
9 results
Semigroups of holomorphic functions; rectifiability and Lipschitz properties of the orbits
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 28 July 2025, pp. 1-30
-
- Article
- Export citation
Schwarz lemma for harmonic functions in the unit ball
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 68 / Issue 2 / May 2025
- Published online by Cambridge University Press:
- 03 February 2025, pp. 616-633
-
- Article
- Export citation
On Harnack inequality and harmonic Schwarz lemma
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 67 / Issue 4 / December 2024
- Published online by Cambridge University Press:
- 10 May 2024, pp. 940-954
- Print publication:
- December 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Entropy of transcendental entire functions
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 2 / February 2021
- Published online by Cambridge University Press:
- 07 October 2019, pp. 338-348
- Print publication:
- February 2021
-
- Article
- Export citation
11 - The ⋆-Function in Complex Analysis
-
- Book:
- Symmetrization in Analysis
- Published online:
- 22 February 2019
- Print publication:
- 14 March 2019, pp 398-453
-
- Chapter
- Export citation
Deforming an є-close-to-hyperbolic metric to a hyperbolic metric
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 148 / Issue 3 / June 2018
- Published online by Cambridge University Press:
- 18 April 2018, pp. 629-641
- Print publication:
- June 2018
-
- Article
- Export citation
Hyperbolic Metric and Multiply Connected Wandering Domains of Meromorphic Functions
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 60 / Issue 3 / August 2017
- Published online by Cambridge University Press:
- 30 January 2017, pp. 787-810
-
- Article
- Export citation
Versions of Schwarz's Lemma for Condenser Capacity and Inner Radius
-
- Journal:
- Canadian Mathematical Bulletin / Volume 56 / Issue 2 / 01 June 2013
- Published online by Cambridge University Press:
- 20 November 2018, pp. 241-250
- Print publication:
- 01 June 2013
-
- Article
-
- You have access
- Export citation
Lipschitz Type Characterizations for Bergman Spaces
-
- Journal:
- Canadian Mathematical Bulletin / Volume 52 / Issue 4 / 01 December 2009
- Published online by Cambridge University Press:
- 20 November 2018, pp. 613-626
- Print publication:
- 01 December 2009
-
- Article
-
- You have access
- Export citation

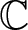
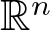
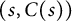
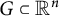
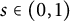
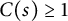
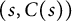

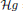 =
= 