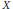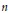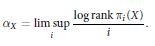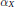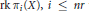Refine search
Actions for selected content:
8 results
SOME RESULTS ON THE TOPOLOGY OF ALGEBRAIC SURFACES
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 258 / June 2025
- Published online by Cambridge University Press:
- 17 February 2025, pp. 376-397
- Print publication:
- June 2025
-
- Article
- Export citation
Leibniz Rule on Higher Pages of Unstable Spectral Sequences
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 61 / Issue 1 / February 2018
- Published online by Cambridge University Press:
- 01 February 2018, pp. 265-282
-
- Article
- Export citation
On the homotopy groups of the self-equivalences of linear spheres
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 59 / Issue 2 / May 2016
- Published online by Cambridge University Press:
- 26 October 2015, pp. 445-462
-
- Article
- Export citation
The Ranks of the Homotopy Groups of a Finite Dimensional Complex
-
- Journal:
- Canadian Journal of Mathematics / Volume 65 / Issue 1 / 01 February 2013
- Published online by Cambridge University Press:
- 20 November 2018, pp. 82-119
- Print publication:
- 01 February 2013
-
- Article
-
- You have access
- Export citation
THE BOUSFIELD–KAN SPECTRAL SEQUENCE FOR MORAVA $K$-THEORY
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 49 / Issue 3 / October 2006
- Published online by Cambridge University Press:
- 25 January 2007, pp. 683-699
-
- Article
-
- You have access
- Export citation
A BANACH SPACE WHOSE OPERATOR ALGEBRA HAS K0-GROUP ℚ
-
- Journal:
- Proceedings of the London Mathematical Society / Volume 84 / Issue 3 / May 2002
- Published online by Cambridge University Press:
- 29 April 2002, pp. 747-768
- Print publication:
- May 2002
-
- Article
- Export citation
A BRAIDED SIMPLICIAL GROUP
-
- Journal:
- Proceedings of the London Mathematical Society / Volume 84 / Issue 3 / May 2002
- Published online by Cambridge University Press:
- 29 April 2002, pp. 645-662
- Print publication:
- May 2002
-
- Article
- Export citation
Shape Fibrations, Multivalued Maps and Shape Groups
-
- Journal:
- Canadian Journal of Mathematics / Volume 50 / Issue 2 / 01 April 1998
- Published online by Cambridge University Press:
- 20 November 2018, pp. 342-355
- Print publication:
- 01 April 1998
-
- Article
-
- You have access
- Export citation