We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
Moduli spaces of real bundles over a real curve arise naturally as Lagrangian submanifolds of the moduli space of semi-stable bundles over a complex curve. In this paper, we adapt the methods of Atiyah–Bott's “Yang–Mills over a Riemann Surface” to compute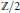 
$\mathbb{Z}/2$–Betti numbers of these spaces.
