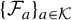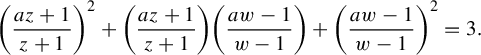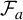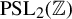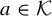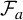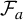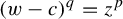Refine search
Actions for selected content:
2 results
Equidistribution for matings of quadratic maps with the modular group
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 3 / March 2024
- Published online by Cambridge University Press:
- 12 May 2023, pp. 859-887
- Print publication:
- March 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Dynamics of hyperbolic correspondences
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 42 / Issue 8 / August 2022
- Published online by Cambridge University Press:
- 04 May 2021, pp. 2661-2692
- Print publication:
- August 2022
-
- Article
- Export citation