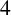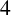Refine search
Actions for selected content:
2 results
A NEW HIGHER ORDER YANG–MILLS–HIGGS FLOW ON RIEMANNIAN
 $4$-MANIFOLDS
$4$-MANIFOLDS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 107 / Issue 2 / April 2023
- Published online by Cambridge University Press:
- 29 November 2022, pp. 320-329
- Print publication:
- April 2023
-
- Article
- Export citation
GRADIENT FLOWS OF HIGHER ORDER YANG–MILLS–HIGGS FUNCTIONALS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 113 / Issue 2 / October 2022
- Published online by Cambridge University Press:
- 31 May 2021, pp. 257-287
- Print publication:
- October 2022
-
- Article
- Export citation