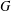Refine search
Actions for selected content:
3 results
THE
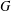 $G$-CENTRE AND GRADABLE DERIVED EQUIVALENCES
$G$-CENTRE AND GRADABLE DERIVED EQUIVALENCES
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 105 / Issue 3 / December 2018
- Published online by Cambridge University Press:
- 18 June 2018, pp. 289-315
- Print publication:
- December 2018
-
- Article
-
- You have access
- Export citation
Abelian Gradings on Upper Block Triangular Matrices
-
- Journal:
- Canadian Mathematical Bulletin / Volume 55 / Issue 1 / 01 March 2012
- Published online by Cambridge University Press:
- 20 November 2018, pp. 208-213
- Print publication:
- 01 March 2012
-
- Article
-
- You have access
- Export citation
Automorphismes, graduations et catégories triangulées
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 10 / Issue 3 / July 2011
- Published online by Cambridge University Press:
- 25 May 2011, pp. 713-751
- Print publication:
- July 2011
-
- Article
- Export citation