We study the gradient superconvergence of bilinear finite volume element (FVE) solving the elliptic problems. First, a superclose weak estimate is established for the bilinear form of the FVE method. Then, we prove that the gradient approximation of the FVE solution has the superconvergence property:
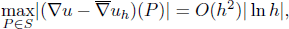
where 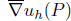 denotes the average gradient on elements containing point P and S is the set of optimal stress points composed of the mesh points, the midpoints of edges and the centers of elements.
denotes the average gradient on elements containing point P and S is the set of optimal stress points composed of the mesh points, the midpoints of edges and the centers of elements.