We show that recent approaches to quantitative analysis based on non-idempotent typing systems can be extended to programming languages with effects. In particular, we consider two cases: the weak open call-by-name (CBN) and call-by-value (CBV) variants of the 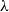$\lambda$-calculus, equipped with operations to write and read from a global state. In order to capture quantitative information with respect to time and space for both CBN and CBV, we design for each of them a quantitative type system based on a (tight) multi-type system. One key observation of this work is how CBN and CBV influence the composition of state types. That is, each type system is developed by taking into account how each language manages the global state: in CBN, the composition of state types is almost straightforward, since function application does not require evaluation of its argument; in CBV, however, the interaction between functions and arguments makes the composition of state types more subtle since only values can be passed as actual arguments. The main contribution of this paper is the design of type systems capturing quantitative information about effectful CBN and CBV programming languages. Indeed, we develop type systems that are qualitatively and quantitatively sound and complete.