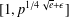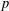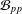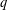Refine search
Actions for selected content:
4 results
ON THE MINIMAL NUMBER OF SMALL ELEMENTS GENERATING FINITE PRIME FIELDS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 96 / Issue 2 / October 2017
- Published online by Cambridge University Press:
- 17 August 2017, pp. 177-184
- Print publication:
- October 2017
-
- Article
-
- You have access
- Export citation
‘ON SETS OF PP-GENERATORS OF FINITE GROUPS’
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 93 / Issue 2 / April 2016
- Published online by Cambridge University Press:
- 05 October 2015, pp. 350-352
- Print publication:
- April 2016
-
- Article
-
- You have access
- Export citation
ON SETS OF PP-GENERATORS OF FINITE GROUPS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 91 / Issue 2 / April 2015
- Published online by Cambridge University Press:
- 14 October 2014, pp. 241-249
- Print publication:
- April 2015
-
- Article
-
- You have access
- Export citation
HALL'S CONDITION AND IDEMPOTENT RANK OF IDEALS OF ENDOMORPHISM MONOIDS
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 51 / Issue 1 / February 2008
- Published online by Cambridge University Press:
- 04 February 2008, pp. 57-72
-
- Article
-
- You have access
- Export citation