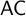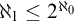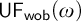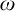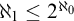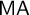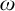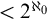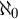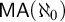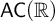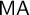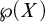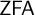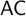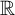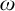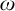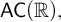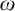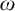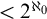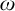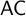In $\mathsf {ZF}$ (i.e., Zermelo–Fraenkel set theory minus the axiom of choice ($\mathsf {AC}$)), we investigate the open problem of the deductive strength of the principle

which was introduced by Herzberg, Kanovei, Katz, and Lyubetsky [(2018), Journal of Symbolic Logic, 83(1), 385–391]. Typical results are:

1. (1) “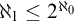$\aleph _{1}\leq 2^{\aleph _{0}}$” is strictly weaker than 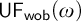$\mathsf {UF_{wob}}(\omega )$ in $\mathsf {ZF}$.

2. (2) “There exists a free ultrafilter on 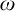$\omega $” does not imply “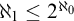$\aleph _{1}\leq 2^{\aleph _{0}}$” in $\mathsf {ZF}$, and thus (by (1)) neither does it imply $\mathsf {UF_{wob}}(\omega )$ in $\mathsf {ZF}$. This fills the gap in information in Howard and Rubin [Mathematical Surveys and Monographs, American Mathematical Society, 1998], as well as in Herzberg et al. (2018).

3. (3) Martin’s Axiom (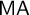$\mathsf {MA}$) implies “no free ultrafilter on 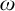$\omega $ has a well-orderable base of cardinality 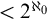$<2^{\aleph _{0}}$”, and the latter principle is not implied by 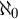$\aleph _{0}$-Martin’s Axiom (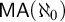$\mathsf {MA}(\aleph _{0})$) in $\mathsf {ZF}$.

4. (4) $\mathsf {MA} + \mathsf {UF_{wob}}(\omega )$ implies 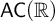$\mathsf {AC}(\mathbb {R})$ (the axiom of choice for non-empty sets of reals), which in turn implies $\mathsf {UF_{wob}}(\omega )$. Furthermore, 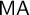$\mathsf {MA}$ and $\mathsf {UF_{wob}}(\omega )$ are mutually independent in $\mathsf {ZF}$.

5. (5) For any infinite linearly orderable set X, each of “every filter base on X can be well ordered” and “every filter on X has a well-orderable base” is equivalent to “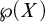$\wp (X)$ can be well ordered”. This yields novel characterizations of the principle “every linearly ordered set can be well ordered” in 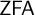$\mathsf {ZFA}$ (i.e., Zermelo–Fraenkel set theory with atoms), and of 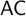$\mathsf {AC}$ in $\mathsf {ZF}$.

6. (6) “Every filter on 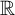$\mathbb {R}$ has a well-orderable base” implies “every filter on 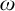$\omega $ has a well-orderable base”, which in turn implies $\mathsf {UF_{wob}}(\omega )$, and none of these implications are reversible in $\mathsf {ZF}$.

7. (7) “Every filter on 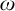$\omega $ can be extended to an ultrafilter with a well-orderable base” is equivalent to 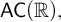$\mathsf {AC}(\mathbb {R}),$ and thus is strictly stronger than $\mathsf {UF_{wob}}(\omega )$ in $\mathsf {ZF}$.

8. (8) “Every filter on 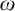$\omega $ can be extended to an ultrafilter” implies “there exists a free ultrafilter on 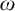$\omega $ which has no well-orderable base of cardinality 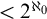${<2^{\aleph _{0}}}$”. The former principle does not imply “there exists a free ultrafilter on 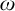$\omega $ which has no well-orderable base” in $\mathsf {ZF}$, and the latter principle is true in the Basic Cohen Model.