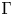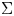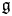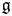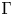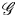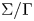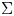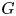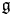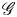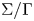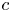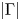Refine search
Actions for selected content:
3 results
Corrigendum: Conformal blocks for Galois covers of algebraic curves
- Part of
-
- Journal:
- Compositio Mathematica / Volume 161 / Issue 4 / April 2025
- Published online by Cambridge University Press:
- 15 August 2025, pp. 945-946
- Print publication:
- April 2025
-
- Article
-
- You have access
- HTML
- Export citation
Conformal blocks for Galois covers of algebraic curves
- Part of
-
- Journal:
- Compositio Mathematica / Volume 159 / Issue 10 / October 2023
- Published online by Cambridge University Press:
- 29 August 2023, pp. 2191-2259
- Print publication:
- October 2023
-
- Article
- Export citation
3 - Factorization Theorem for Space of Vacua
-
- Book:
- Conformal Blocks, Generalized Theta Functions and the Verlinde Formula
- Published online:
- 19 November 2021
- Print publication:
- 25 November 2021, pp 83-124
-
- Chapter
- Export citation