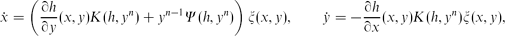Search

1 - Introduction
M. J. D. Hamilton, Universität Stuttgart, D. Kotschick, Ludwig-Maximilians-Universität München
Book:

Künneth Geometry

Published online:

07 December 2023

Print publication:

21 December 2023, pp 1-12
- Chapter
- - Get access
    
    Check if you have access via personal or institutional login
    
    Log in Register
- Export citation
Summary

This book is about the geometry and topology of symplectic manifolds equipped with pairs of complementary Lagrangian foliations. The resulting structure is very rich, intertwining symplectic geometry, the theory of foliations, dynamical systems, and pseudo-Riemannian geometry in interesting ways.
Before describing the contents of the book in detail, we want to discuss a few motivating vignettes. The first two of these are to be kept in mind as motivational background, whereas the third and fourth ones will be taken up again and again later in the book.

Rigid centres on the center manifold of tridimensional differential systems
Part of
- Qualitative theory
- General theory in ordinary differential equations
Adam Mahdi, Claudio Pessoa, Jarne D. Ribeiro
Journal:

Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 152 / Issue 4 / August 2022

Published online by Cambridge University Press:

07 September 2021, pp. 1058-1080

Print publication:

August 2022
- Article
- - Get access
    
    Check if you have access via personal or institutional login
    
    Log in Register
- Export citation
Motivated by the definition of rigid centres for planar differential systems, we introduce the study of rigid centres on the center manifolds of differential systems on $\mathbb {R}^{3}$. On the plane, these centres have been extensively studied and several interesting results have been obtained. We present results that characterize the rigid systems on $\mathbb {R}^{3}$ and solve the centre-focus problem for several families of rigid systems.

A note on analytic integrability of planar vector fields
A. ALGABA, C. GARCÍA, M. REYES
Journal:

European Journal of Applied Mathematics / Volume 23 / Issue 5 / October 2012

Published online by Cambridge University Press:

23 April 2012, pp. 555-562
- Article
- - Get access
    
    Check if you have access via personal or institutional login
    
    Log in Register
- Export citation
We give a new characterisation of integrability of a planar vector field at the origin. This allows us to prove that the analytic systemswhere h, K, Ψ and ξ are analytic functions defined in the neighbourhood of O with K(O) ≠ 0 or Ψ(O) ≠ 0 and n ≥ 1, have a local analytic first integral at the origin. We show new families of analytically integrable systems that are held in the above class. In particular, this class includes all the nilpotent and generalised nilpotent integrable centres that we know.

Search Results