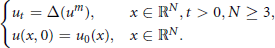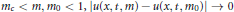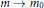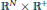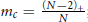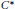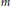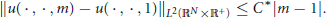The Continuous Dependence on the Nonlinearities of Solutions of Fast Diffusion Equations
-
- Journal:
- Canadian Mathematical Bulletin / Volume 55 / Issue 3 / 01 September 2012
- Published online by Cambridge University Press:
- 20 November 2018, pp. 623-631
- Print publication:
- 01 September 2012
-
- Article
-
- You have access
- Export citation
-
In this paper, we consider the Cauchy problem
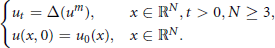\left\{ \begin{align} & {{u}_{t}}=\Delta ({{u}^{m}}),\,\,\,\,\,x\in {{\mathbb{R}}^{N}},t>0,N\ge 3, \\ & u(x,0)={{u}_{0}}(x),\,\,\,\,\,x\in {{\mathbb{R}}^{N}}. \\ \end{align} \right.We will prove that
(i) for 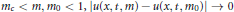{{m}_{c}}\,<\,m,\,{{m}_{0}}\,<\,1,\,\left| u(x,\,t,m)-u(x,\,t,{{m}_{0}}) \right|\,\to \,0 as 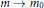m\,\to \,{{m}_{0}} uniformly on every compact subset of 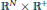{{\mathbb{R}}^{N}}\,\times \,{{\mathbb{R}}^{+}}, where 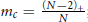{{m}_{c}}\,=\,\frac{{{(N-2)}_{+}}}{N};
(ii) there is a 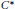{{C}^{*}} that explicitly depends on 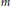m such that
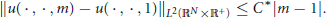{{\left\| u(\cdot ,\cdot ,m)-u(\cdot ,\cdot ,1) \right\|}_{{{L}^{2}}({{\mathbb{R}}^{N}}\times {{\mathbb{R}}^{+}})}}\le {{C}^{*}}\left| m-1 \right|.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
