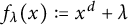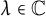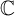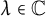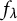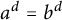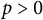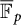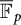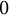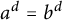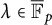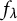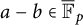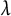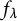In the goundbreaking paper [BD11] (which opened a wide avenue of research regarding unlikely intersections in arithmetic dynamics), Baker and DeMarco prove that for the family of polynomials 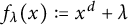$f_\lambda (x):=x^d+\lambda $ (parameterized by 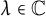$\lambda \in \mathbb {C}$), given two starting points a and b in 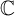$\mathbb {C}$, if there exist infinitely many 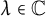$\lambda \in \mathbb {C}$ such that both a and b are preperiodic under the action of 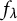$f_\lambda $, then 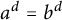$a^d=b^d$. In this paper, we study the same question, this time working in a field of characteristic 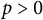$p>0$. The answer in positive characteristic is more nuanced, as there are three distinct cases: (i) both starting points a and b live in 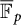${\overline {\mathbb F}_p}$; (ii) d is a power of p; and (iii) not both a and b live in 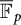${\overline {\mathbb F}_p}$, while d is not a power of p. Only in case (iii), one derives the same conclusion as in characteristic 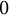$0$ (i.e., that 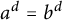$a^d=b^d$). In case (i), one has that for each 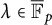$\lambda \in {\overline {\mathbb F}_p}$, both a and b are preperiodic under the action of 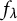$f_\lambda $, while in case (ii), one obtains that also whenever 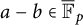$a-b\in {\overline {\mathbb F}_p}$, then for each parameter 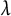$\lambda $, we have that a is preperiodic under the action of 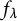$f_\lambda $ if and only if b is preperiodic under the action of 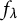$f_\lambda $.