Let 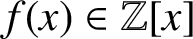 $f(x)\in \mathbb {Z}[x]$
be a nonconstant polynomial. Let
$f(x)\in \mathbb {Z}[x]$
be a nonconstant polynomial. Let 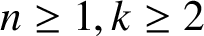 $n\ge 1, k\ge 2$
and c be integers. An integer a is called an f-exunit in the ring
$n\ge 1, k\ge 2$
and c be integers. An integer a is called an f-exunit in the ring 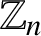 $\mathbb {Z}_n$
of residue classes modulo n if
$\mathbb {Z}_n$
of residue classes modulo n if 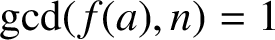 $\gcd (f(a),n)=1$
. We use the principle of cross-classification to derive an explicit formula for the number
$\gcd (f(a),n)=1$
. We use the principle of cross-classification to derive an explicit formula for the number 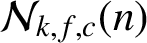 ${\mathcal N}_{k,f,c}(n)$
of solutions
${\mathcal N}_{k,f,c}(n)$
of solutions  $(x_1,\ldots ,x_k)$
of the congruence
$(x_1,\ldots ,x_k)$
of the congruence 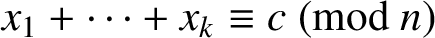 $x_1+\cdots +x_k\equiv c\pmod n$
with all
$x_1+\cdots +x_k\equiv c\pmod n$
with all 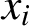 $x_i$
being f-exunits in the ring
$x_i$
being f-exunits in the ring 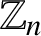 $\mathbb {Z}_n$
. This extends a recent result of Anand et al. [‘On a question of f-exunits in
$\mathbb {Z}_n$
. This extends a recent result of Anand et al. [‘On a question of f-exunits in 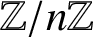 $\mathbb {Z}/{n\mathbb {Z}}$
’, Arch. Math. (Basel)116 (2021), 403–409]. We derive a more explicit formula for
$\mathbb {Z}/{n\mathbb {Z}}$
’, Arch. Math. (Basel)116 (2021), 403–409]. We derive a more explicit formula for 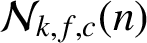 ${\mathcal N}_{k,f,c}(n)$
when
${\mathcal N}_{k,f,c}(n)$
when 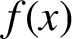 $f(x)$
is linear or quadratic.
$f(x)$
is linear or quadratic.
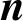 $\boldsymbol {n}$
$\boldsymbol {n}$
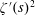 $\unicode[STIX]{x1D701}^{\prime }(s)^{2}$,
$\unicode[STIX]{x1D701}^{\prime }(s)^{2}$, 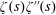 $\unicode[STIX]{x1D701}(s)\unicode[STIX]{x1D701}^{\prime \prime }(s)$, and
$\unicode[STIX]{x1D701}(s)\unicode[STIX]{x1D701}^{\prime \prime }(s)$, and 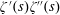 $\unicode[STIX]{x1D701}^{\prime }(s)\unicode[STIX]{x1D701}^{\prime \prime }(s)$
$\unicode[STIX]{x1D701}^{\prime }(s)\unicode[STIX]{x1D701}^{\prime \prime }(s)$