No CrossRef data available.
Article contents
Titchmarsh’s Method for the Approximate Functional Equations for 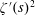 $\unicode[STIX]{x1D701}^{\prime }(s)^{2}$,
$\unicode[STIX]{x1D701}^{\prime }(s)^{2}$, 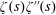 $\unicode[STIX]{x1D701}(s)\unicode[STIX]{x1D701}^{\prime \prime }(s)$, and
$\unicode[STIX]{x1D701}(s)\unicode[STIX]{x1D701}^{\prime \prime }(s)$, and 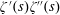 $\unicode[STIX]{x1D701}^{\prime }(s)\unicode[STIX]{x1D701}^{\prime \prime }(s)$
$\unicode[STIX]{x1D701}^{\prime }(s)\unicode[STIX]{x1D701}^{\prime \prime }(s)$
Published online by Cambridge University Press: 09 January 2019
Abstract
Let 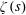 $\unicode[STIX]{x1D701}(s)$ be the Riemann zeta function. In 1929, Hardy and Littlewood proved the approximate functional equation for
$\unicode[STIX]{x1D701}(s)$ be the Riemann zeta function. In 1929, Hardy and Littlewood proved the approximate functional equation for 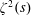 $\unicode[STIX]{x1D701}^{2}(s)$ with error term
$\unicode[STIX]{x1D701}^{2}(s)$ with error term 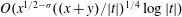 $O(x^{1/2-\unicode[STIX]{x1D70E}}((x+y)/|t|)^{1/4}\log |t|)$, where
$O(x^{1/2-\unicode[STIX]{x1D70E}}((x+y)/|t|)^{1/4}\log |t|)$, where 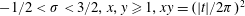 $-1/2<\unicode[STIX]{x1D70E}<3/2,x,y\geqslant 1,xy=(|t|/2\unicode[STIX]{x1D70B})^{2}$. Later, in 1938, Titchmarsh improved the error term by removing the factor
$-1/2<\unicode[STIX]{x1D70E}<3/2,x,y\geqslant 1,xy=(|t|/2\unicode[STIX]{x1D70B})^{2}$. Later, in 1938, Titchmarsh improved the error term by removing the factor 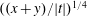 $((x+y)/|t|)^{1/4}$. In 1999, Hall showed the approximate functional equations for
$((x+y)/|t|)^{1/4}$. In 1999, Hall showed the approximate functional equations for 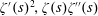 $\unicode[STIX]{x1D701}^{\prime }(s)^{2},\unicode[STIX]{x1D701}(s)\unicode[STIX]{x1D701}^{\prime \prime }(s)$, and
$\unicode[STIX]{x1D701}^{\prime }(s)^{2},\unicode[STIX]{x1D701}(s)\unicode[STIX]{x1D701}^{\prime \prime }(s)$, and 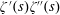 $\unicode[STIX]{x1D701}^{\prime }(s)\unicode[STIX]{x1D701}^{\prime \prime }(s)$ (in the range
$\unicode[STIX]{x1D701}^{\prime }(s)\unicode[STIX]{x1D701}^{\prime \prime }(s)$ (in the range 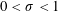 $0<\unicode[STIX]{x1D70E}<1$) whose error terms contain the factor
$0<\unicode[STIX]{x1D70E}<1$) whose error terms contain the factor 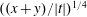 $((x+y)/|t|)^{1/4}$. In this paper we remove this factor from these three error terms by using the method of Titchmarsh.
$((x+y)/|t|)^{1/4}$. In this paper we remove this factor from these three error terms by using the method of Titchmarsh.
MSC classification
Information
- Type
- Article
- Information
- Copyright
- © Canadian Mathematical Society 2018
Footnotes
This work was supported by JSPS KAKENHI: 26400030, 15K17512 and 15K04778.

