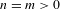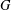Refine search
Actions for selected content:
6 results
11 - Traces and ultraproducts
-
- Book:
- Tensor Products of <I>C</I>*-Algebras and Operator Spaces
- Published online:
- 10 February 2020
- Print publication:
- 27 February 2020, pp 225-261
-
- Chapter
- Export citation
Finite-dimensional approximations for Nica–Pimsner algebras
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 40 / Issue 12 / December 2020
- Published online by Cambridge University Press:
- 09 August 2019, pp. 3375-3402
- Print publication:
- December 2020
-
- Article
- Export citation
EMBEDDINGS AND
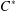 $C^{\ast }$ -ENVELOPES OF EXACT OPERATOR SYSTEMS
$C^{\ast }$ -ENVELOPES OF EXACT OPERATOR SYSTEMS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 96 / Issue 2 / October 2017
- Published online by Cambridge University Press:
- 02 May 2017, pp. 274-285
- Print publication:
- October 2017
-
- Article
-
- You have access
- Export citation
FIXED POINT CHARACTERISATION FOR EXACT AND AMENABLE ACTION
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 92 / Issue 2 / October 2015
- Published online by Cambridge University Press:
- 16 June 2015, pp. 228-232
- Print publication:
- October 2015
-
- Article
-
- You have access
- Export citation
A Note on the Exactness of Operator Spaces
-
- Journal:
- Canadian Mathematical Bulletin / Volume 53 / Issue 2 / 01 June 2010
- Published online by Cambridge University Press:
- 20 November 2018, pp. 239-246
- Print publication:
- 01 June 2010
-
- Article
-
- You have access
- Export citation
Amalgamated free products of C*-bundles
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 52 / Issue 1 / February 2009
- Published online by Cambridge University Press:
- 02 February 2009, pp. 23-36
-
- Article
-
- You have access
- Export citation